0x02 简单类型Lambda演算系统 - 函数式类型系统

Makabaka18802025年6月17日...大约 12 分钟

0x02 简单类型Lambda演算系统 - 函数式类型系统

本节术语 | Glossary

图灵机 (Turing's machine) 利用无限长的纸带和读写头搭建的计算模型
λ演算 (The Lambda Calculus) 利用无限长的纸带和读写头搭建的计算模型
简单类型λ演算 (STLC) 一种带有简单chaining的类型系统
上下文 (Context) 关联变量及其类型的数据结构
作用域 (Scope) 一种在程序语言中上下文的实现
类型判断 (Type Judgement) 通过类型系统来验证程序的合理性

让我们把时间拨回100年前。

二战时期，英国出现了一位数学家叫图灵:

他发明了个特别著名的模型叫图灵机 —— 通过无限长的纸带和读写头，精确定义了"可计算性"的概念。

图灵机

图灵机 (Turing Machine) 是艾伦·图灵1936年提出的计算模型，由以下组件构成：

M = (Q, \Sigma, \Gamma, \delta, q_0, q_{\text{accept}}, q_{\text{reject}})

组件	符号	说明
状态集	$Q$	有限状态集合
输入字母表	$\Sigma$	允许的输入符号集合
纸带字母表	$\Gamma$	$\Sigma \subset \Gamma$
转移函数	$\delta$	$Q \times \Gamma \to Q \times \Gamma \times \{L,R\}$
初始状态	$q_0 \in Q$	计算起始点
接受状态	$q_{\text{accept}}$	计算成功终止状态
拒绝状态	$q_{\text{reject}}$	计算失败终止状态

读写头 扫描纸带当前单元格
根据 当前状态 $q_i$ 和 读取符号 $s$ 查表
执行 $\delta(q_i, s) = (q_j, s', D)$ $δ (q_{i}, s) = (q_{j}, s^{'}, D)$ ：
- 将状态改为 $q_j$
- 写入符号 $s'$ 到当前单元格
- 按方向 $D$ (左移L/右移R)移动读写头

但鲜为人知的是，他的导师美国数学家阿隆佐·邱奇（Alonzo Church） 提出了另一种等效的计算模型：Lambda Calculus.

λ演算

λ演算 (Lambda Calculus) 是阿隆佐·邱奇(Alonzo Church)在1930年代提出的形式系统，构成了函数式编程的理论基础。

深入探索λ演算 →

其核心只有三条语法规则：

<表达式> ::= <变量>                 (变量)
          | λ<变量>.<表达式>       (抽象)
          | <表达式> <表达式>      (应用)

概念	表示	示例	说明
α转换	$\lambda x.\ M \to \lambda y.\ M[x:=y]$	$\lambda x.\ x \to \lambda y.\ y$	变量重命名
β归约	$(\lambda x.\ M)\ N \to M[x:=N]$	$(\lambda x.\ x)\ y \to y$	函数应用
η变换	$\lambda x.\ (M\ x) \to M$	$\lambda x.\ (f\ x) \to f$	函数等价简化

其重要的特性包含

图灵完备：可表达任何可计算函数
无类型系统：原始版本无类型约束
柯里化：多参函数转化为嵌套λ：
f(x,y) = x+y ⇨ λx.λy.x+y

在现实中，其应用包括

函数式语言核心(Haskell/Lisp)
编程语言理论基石
编译器优化基础

但是这个东西有个缺陷：lambda演算毫无安全性可言，正如图灵机的类型只有其字母表一样。尽管这样可以实现类似c++当中用指针当泛型的神奇操作，但还是太不实用了。于是在不久后，邱奇就提出了STLC (Simply-Typed Lambda Calculus).

建议

一下内容将建立在读者熟悉λ演算的前提上。若读者未了解过其，建议先学习一下函数式编程或者λ演算
学习λ演算 →

我们先从一个简单的函数来看吧:

\lambda x.\ x

类型系统首先需要知道每个变量的类型是啥；这时我们需要一个上下文 (Context)。数学上来说，是我们的程序当中所有绑定变量 $x$ 与其类型 $\tau$ 所形成的有序对的集合:

\Gamma = \{(x, \tau) | \forall x\}

当然对于软件工程师来说可能这样更好理解一点：

context = {x: type(x) for x in variables}

它干的是啥呢？就是把每一个在这个范围内的变量还有他的类型拉了一张表。（现在很多的解释器和编译器也会那么干）

而我们一般这样来表示一个有序对：

let x: τ;

等价于

x:\tau \in \Gamma

在软件工程中，上下文的概念实现为作用域 (Scope)。大多数语言都有作用域：

Swift

let a = 10;
let _: Int = {
    let b = 20;
    type(of: a);    // Int.Type = Int
    type(of: b);    // Int.Type = Int
}()
type(of: a);        // Int.Type = Int
type(of: b);        // Error: cannot find 'b' in scope

ECMAScript / JS

const a = 10;
{
    const b = 20;
    typeof a;       // 'number'
    typeof b;       // 'number'
}
typeof a;           // 'number'
typeof b;           // undefined

Haskell

let x = 10 in
  let x = 20 in
    print x  -- prints 20
-- Outer x still refers to 10 in other expressions

最常见的作用域就是函数定义了，我们在函数里面的参数啊、定义的变量啊在出了函数定义的作用域之后就无法再次使用了：

def add(a, b):
    sum = a + b
    return sum

a, b = 1, 2
c = add(a, b)
print(a, b, c)  # All global, defined under context Γ
print(sum)      # NameError: sum is defined in the scope of the function declaration, and is not reachable outside that scope.

而我们可以根据上下文来进行类型判断 (Type Judgement):

\Gamma \vdash x:\tau

即

assert(type(x) == τ.Type)

简单来说，就是判断一个项 / 变量 $x$ 的类型是否为 $\tau$ .

一般来说，我们在STLC中解决的问题都是求解一个对象的类型。接下来，我们介绍三条对于STLC我们常用的Type Check规则。

记法风格约定

在接下来的逻辑推理与类型证明中，我们将交替使用以下三种常见的记法风格：

说明：本教材默认使用 形式推理（自然演绎）风格进行主要推导，必要时补充其它格式以增强理解。

初等证明格式

用于日常数学中的条件推导，适合简明陈述前提与结论：

\begin{align*} &\because\ a > b,\ \text{且}\ b > c \\ &\therefore\ a > c \end{align*}

递等式推导

常用于 λ-演算、类型变换等语法结构的推导，强调等价关系：

\begin{align*} (\lambda y.\ \lambda x.\ x)\ f &\to^{\beta} (\lambda x.\ x)[f / y] \\ &= \lambda x.\ x \equiv I \end{align*}

形式推理（自然演绎）

强调结构化地描述推理规则，适合系统化描述类型演绎：

\dfrac{ \Gamma \vdash a \to b \quad \Gamma \vdash b \to c }{ \Gamma \vdash a \to c }

I. 变量规则

\dfrac{x:\tau \in \Gamma}{\Gamma \vdash x : \tau}

这条规则说的是，假设我们有一个变量，类型为 $\tau$ , 且这条记录在context中，那么context中一定x对应 $\tau$ 。看似是废话，但实际上说明了变量的类型取决于上下文，这也就是静态类型语言的要求。

工程应用

若我们在一个上下文中声明了

var id: Int;

那我们就能保证操作

id += 1;

是类型安全操作，因为在这个上下文的所有地方，x的类型都是Int，不会突然变成Bool或者其他类型。

之所以没有保证这是安全操作就是因为可能Int会溢出或者遇到其他软件工程错误，但这不是这篇文章的范畴了

II. 抽象规则

\dfrac{(\Gamma + x:\tau_1) \vdash M : \tau_2}{\Gamma \vdash (\lambda x:\tau_1. M) : \tau_1 \to \tau_2}

翻译成自然语言就是：如果对于上下文 $\Gamma$ 拓展成一个新的上下文 $\Gamma'$ ，并在其中定义了 $x$ 的类型为 $\tau_1$ ，同时这种情况下 $M$ 的类型为 $\tau_2$ ，那么 $\lambda x.\ M$ 在 $\Gamma'$ 的类型就是 $\tau_1 \to \tau_2$ .

对于实际应用来说，这种拓展可以在一个作用域内看作建立一个新的作用域，这里用swift的闭包做演示：

// Context Γ
var a: SomeType  // Global variable in context Γ

// Define a lambda abstraction: λx: τ1. M
// This is a *function value* of type τ1 → τ2, assigned to the variable `lambda_x_dot_M`
let lambda_x_dot_M: (τ1) -> τ2 = { (x: τ1) -> τ2 in
    // In extended context Γ' = Γ ∪ {x: τ1}, we define M of type τ2
    let M: τ2 = someOp(x)  // some operation that uses x to produce a τ2
    return M               // return M, so the function maps τ1 input to τ2 output
}

Swift的闭包内可以看作一个继承了所有全局的上下文中的类型信息，也就是说在闭包lambda_x_dot_M当中，a也有SomeType类型。但是闭包内的上下文( $\Gamma$ )完全是一份独立于全局上下文的副本( $\Gamma'$ )，所以在这里面添加的信息都无法在外部获得。

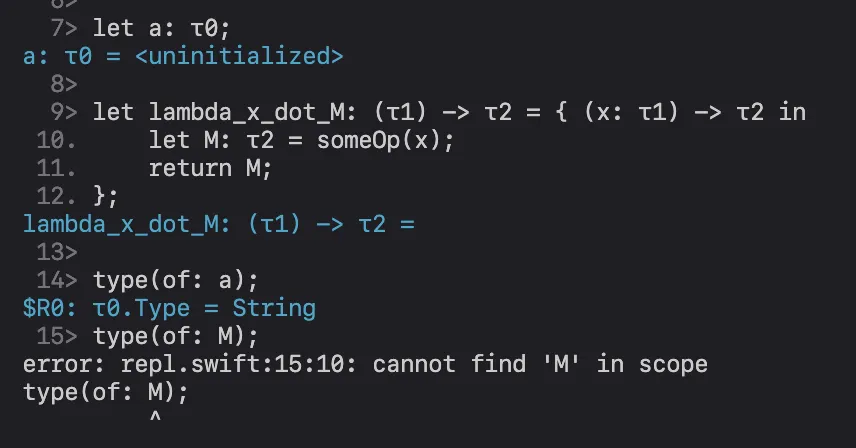
14行和15行就是在全局上下文中进行的，可以看到中定义的可以获取到，但是中的就获取不到 — 14行和15行就是在全局上下文 $\Gamma$ 中进行的，可以看到 $\Gamma$ 中定义的`a`可以获取到，但是 $\Gamma'$ 中的`M`就获取不到

在现实中，写这种闭包还是不够直观。所以一般我们会使用封装函数 (Procedurals)来保证开发效率的同时使用副作用 (Side-effects)来提高程序效率。这可能会牺牲程序安全性，但这点风险在现实工程实现中完全可以忽略不计。

Swift

func equivalent_of_lambda_x_dot_M(x: τ1) -> τ2 {    // Function takes in a parameter of type τ1
    let M: τ2 = someOp(x); return M; // Computes something to return sth of type τ2
}

C++

τ2 equivalent_of_lambda_x_dot_M(τ1 x) {
    τ2 M = someOp(x); return M;
}

总体来说，抽象规则可以如下进行：

工程应用

假设我们需要一个加密凯撒码的方法。我们假设前端已经预先过滤掉了不合理的输入，后端现在所需要进行的操作就是将它们全部进行相应的位移。

void encryptString(char *s, int shift) {
    for (int i = 0; s[i] != '\0'; i++) {
        char base = isupper(s[i]) ? 'A' : 'a';
        s[i] = (s[i] - base + shift) % 26 + base;
    }
}

不难发现，我们先前一直以为是类型不安全的C语言实际上可以通过其他的约束来实现安全性。由于其字符与整形几乎完全等价，C在此时甚至能提供更多的便利性。在实际软件工程学中，我们对于安全性的保证不仅仅是对于语言本身的类型系统的要求；更是架构以及程序的优良设计的需求。

III. 应用规则

\dfrac{ \Gamma \vdash f:\ \tau_1 \to \tau_2 \quad \Gamma \vdash x:\ \tau_1 } { \Gamma \vdash f (x):\ \tau_2 }

在自然语言当中，这说明如果有一个函数f有类型 $\tau_1 \to \tau_2$ , 那么将其作用于一个项 $x:\ \tau_1$ 上将会得到一个类型为 $\tau_2$ 的项。这很好理解吧，一个吃进去 $\tau_1$ 吐出来 $\tau_2$ 的函数，吃进去了一个 $\tau_1$ 一定会吐出来 $\tau_2$ 。

还是用Swift闭包做演示：

func f(_ param: τ1) -> τ2 {
    return someOp(param)        // This value is gaurunteed by the compiler to be of type τ2
}

let x: τ1 = .someValueOfTau1    // Ad-hoc constructor only for demonstration
let M = f(for: x); type(of: M)  // type is τ2

工程应用

假设我们通过enum定义了一个和类型(Sum Type)Department, 它有三个值：.admin, .engineering, .product, 那么通过定义以下函数我们就可以保证一个对于任意部门都输出合理输出的描述函数：

enum Department {
    case admin
    case engineering
    case product
}

let description: (Department) -> String = { (department: Department) -> String in
    switch department {
    case .admin:
        return "Administrative department coordinates the entire group."
    case .engineering:
        return "Engineering department is the core of developing new products"
    case .product:
        return "Product department ensures the market value of the groups' products"
    }
}

这个闭包的类型是 Department -> String，说明对于每个输入值 Department，它都能返回一个确定的 String 类型的输出。这种映射在类型系统中是严格静态可检查的 —— 只要输入的类型是 Department，输出就一定是 String，符合应用规则中的 $\tau_1 \to \tau_2$ 类型约束。

更进一步，由于 Department 是一个封闭的枚举类型（和类型），其所有可能的构造子都已在类型定义中列明，因此 switch 语句在本质上就是对 $\tau_1$ 的所有可能情况进行穷尽分析（exhaustive matching）。也就是说，表达式 $M$ 在 $\lambda x^{\tau_1}.\ M$ 中不会在任何合法输入下失败，因此整个函数的类型 $\tau_1 \to \tau_2$ 是可验证且总是安全的。

在后续的章节中，我们会了解到由于 Department 是一个封闭的枚举（和）类型，其所有可能的构造子在类型定义中已经列出，因此 switch 语句本质上就是对 $\tau_1$ 的所有可能值进行“语义完备”的处理，使得 $\lambda x^{\tau_1}.\ M$ 的 M 不会在任何合法输入下失效，从而确保整个函数的类型是严格可验证的 $\tau_1 \to \tau_2$ 。

IV. 应用

在现实情况中，STLC的逻辑被LSP Server、 linter以及编译器所广泛使用。让我们来看看一个编译器是如何验证一个函数类型的吧：

let identityTwice: (Int) -> Int { (x: Int) ->
    let id: (Int) -> Int = { $0 };
    return id(id(x))
}

我们在里面看到两个类型声明：

$\Gamma \vdash \text{identityTwice}:\ \text{Int} \to \text{Int}$
$\Gamma \vdash \text{id}:\ \text{Int} \to \text{Int}$

我们来依次证明吧！首先，我们可以将这个闭包写成一个lambda抽象体：

\text{identityTwice} = \lambda x^{\text{Int}}.\ \text{id}(\text{id}(x))

我们先来分析 $\text{id}$ .

\text{id} = \lambda x^{\text{Int}}.\ x

熟悉lambda演算的同学应该一眼就可以看出来这是恒等函数，会原样返回本来输入的项。因此，其输入和返回应该是一样的，所以第二条声明是合理的。

我们接下来来分析这个闭包本身。我们进入内部，声明一个拓展上下文：

\Gamma' = \Gamma + x:\ \text{Int}

我们再来看本来的抽象体

\text{identityTwice} = \lambda x^{\text{Int}}.\ \text{id}(\text{id}(x))

引理 1. 对于 $\forall x:\ \text{Int} \in \Gamma,\ \Gamma \vdash \text{id}(x):\ \text{Int}$ .
证明.

\dfrac{ \dfrac{ ( \Gamma \vdash id: \text{Int} \to \text{Int}) \quad (\Gamma' \subset \Gamma) } { \Gamma' \vdash id: \text{Int} \to \text{Int} } \quad \Gamma' \vdash x:\text{Int} }{ \Gamma' \vdash \text{id}(x):\text{Int} }

引理2. $\text{identityTwice}$ 与 $\text{id}$ 等价

证明. 我们可以对着这个双层id一通展开：

\begin{align*} \text{identityTwice} &= \lambda x^{\text{Int}}.\ \text{id}(\text{id}(x)) \\ &= \lambda x^{\text{Int}}.\ (\lambda y^{\text{Int}}.\ y)((\lambda z^{\text{Int}}.\ z)(x)) \\ &\to^{\beta} \lambda x^{\text{Int}}.\ (\lambda y^{\text{Int}}.\ y)(x) \\ &\to^{\beta} \lambda x^{\text{Int}}.\ x \equiv \text{id} \end{align*}

注意到， $\text{id}$ 的类型是int -> int, 所以 $\text{identityTwice}$ 的类型也是int -> int。证毕。

优雅～

(未完待续)

你认为这篇文章怎么样？

昵称

邮箱

网址

按正序
按倒序
按热度

0x02 简单类型Lambda演算系统 - 函数式类型系统

0x02 简单类型Lambda演算系统 - 函数式类型系统

I. 变量规则

II. 抽象规则

III. 应用规则

IV. 应用

预览: