库仑定律与静电场

和电流相对的就是静电，单独的电荷。我们一般在冬天被电到也是因为静电电荷形成的电势差导致的。

静电荷

在自然界中，一个电荷可以是一个电子或者一个质子。

质子

质子 (Proton) 是一种自然界中的电荷，携带正电荷。它的电荷量为 $+1.602 \times 10^{-19}$ 库伦。质子存在于原子核中，能够形成静电荷。当质子失去电子时，它形成一个正的静电荷。

电子

电子 (Electron) 是一种自然界中的电荷，携带负电荷。它的电荷量为 $-1.602 \times 10^{-19}$ 库伦。电子围绕原子核运动，能够形成静电荷。当电子被孤立时，它会产生负的静电荷。

中子

中子 (Neutron) 并不是一种电荷。它不携带电荷，然而在原子核中，中子的存在对于稳定核结构至关重要，因为它能有效防止质子之间的电荷排斥力，从而保持原子核的稳定。

就像在物理课中说过的一样，同种电荷相互排斥，但为什么呢？

库仑定律

我们都知道重力场呈平方反比律：

平方反比律

平方反比律 (Inverse Square Law) 是一种物理定律，表明某些物理量（如光强、引力、静电力等）与距离的平方成反比。这意味着随着距离的增大，这些物理量的强度会迅速减弱。平方反比律的来源可以追溯到点源的辐射或力的分布。在三维空间中，随着距离的增加，能量或力的“分布面积”以平方比例增加，因此强度会减弱为距离的平方反比。如下图中，场的强被均匀的散在了$a^2$与$b^2$的球面上，因此场强之比为$a^{-2} : b^{-2}$, 顾$\mathbf{F}(l) \varpropto \frac{1}{l^2}$

Inverse Square Law Diagram

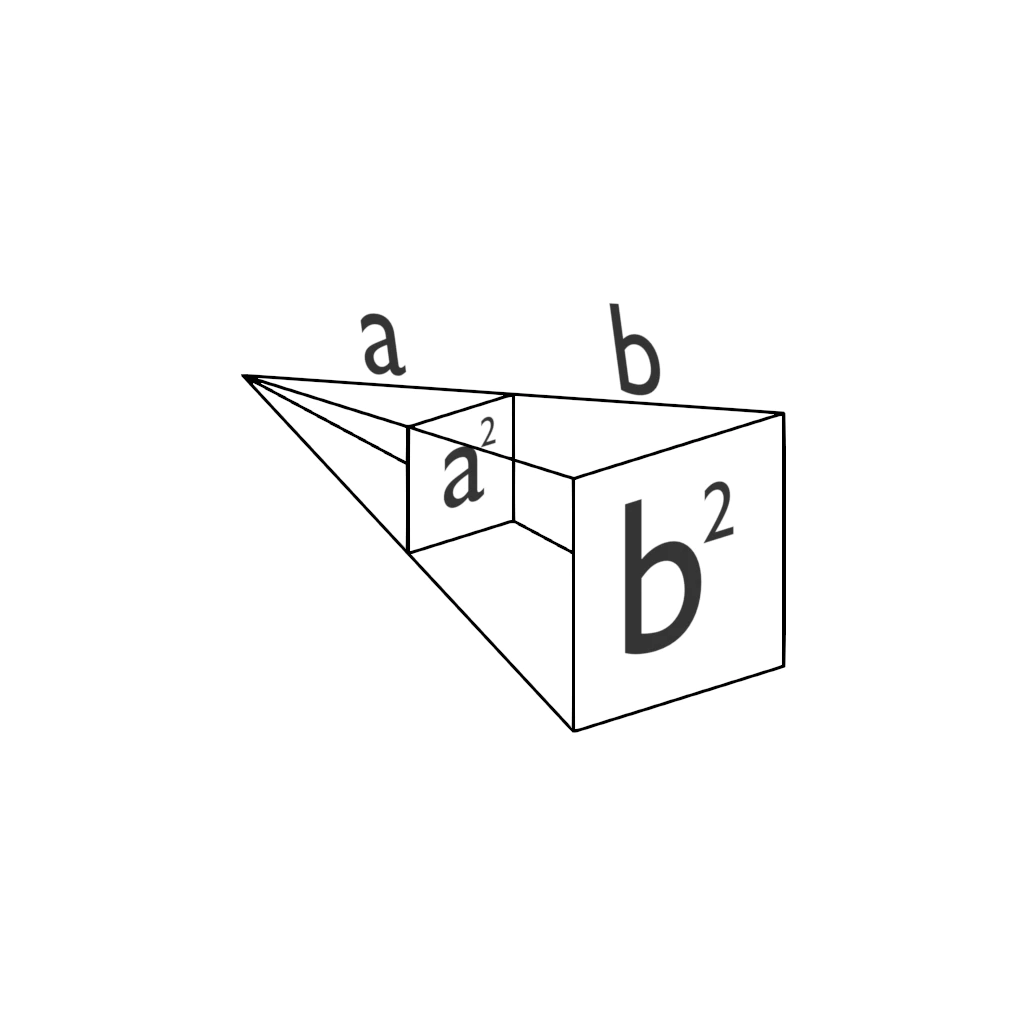
由于电场也是由一个点发散的，所以它也符合平方反比律。我们假设距$q_1$的距离为$r$:

$$\mathbf{E_{q_1}}(l) \varpropto \frac{1}{r^2}$$

由于电场也与电荷量$q$呈正比:

$$\mathbf{E_{q_1}}(l) \varpropto q_1$$

因此我们知道电场一定是以下形式，其中$k$是一个常数:

$$\mathbf{E_{q_1}}(l) = k\frac{q_1}{r^2}$$

这只是一个电荷的电场，未免有点无聊。如果我们想要得到两个电荷$q_1$和$q_2$之间的互作用，那就需要探讨电场对于电荷的力怎么计算了。

接下来，我们可以通量纲分析，发现电场的量纲是力除以电荷，单位是$\mathrm{N/C}$. 也就是说，要得到电场力，我们就要用电场$E_{q_1}$乘以电荷$q_2$的电荷量：

$$\mathbf F = k\frac{q_1}{r^2} \cdot q_1$$

其中, $k$一般写作$k_e$. 它有个特殊的名字，库仑常数。一般来说，$k_e = 8.9875 \times 10^9 \mathrm{N \cdot m^2 / C^2}$, 这个值是托马斯·杨等实验测定的。

多个电荷的情况

这是一个有趣的仿真练习；好奇的可以去看看这里。重力场由于也是可以线性叠加的平方反比场，所以仿真和静电场是一样的，所以我就拿来那里的代码直接用了。

代码

答题思路是OOP，创建了一个class Charge来储存单个电荷的信息，还有一个class ElectricField来储存总电场。具体算法是通过遍历场景的Charge物体，然后一个一个进行叠加来计算总电场。

import bpy
from typing import Tuple, List
from math import sqrt

s = 4

# Helper Funcs
def assign_emission_shader(name, color, obj, strength=1.0):
    """
    Assign an emission shader with the specified color and strength to the given object.
    
    Parameters:
    - name: The name of the material to be created.
    - color: The RGB color for the emission shader (a tuple like (1.0, 0.0, 0.0) for red).
    - obj: The Blender object to which the material will be assigned.
    - strength: The strength of the emission (default is 1.0).
    """
    # Check if the object already has the material assigned
    existing_material = bpy.data.materials.get(name)
    
    # If the material doesn't exist, create a new one
    if not existing_material:
        material = bpy.data.materials.new(name)  # Create the material
        material.use_nodes = True  # Enable the use of nodes
        nodes = material.node_tree.nodes
        
        # Clear existing nodes
        for node in nodes:
            nodes.remove(node)
        
        # Add an Emission shader node
        emission_node = nodes.new(type='ShaderNodeEmission')
        emission_node.inputs['Color'].default_value = (*color, 1.0)  # Set the color with alpha = 1
        emission_node.inputs['Strength'].default_value = strength  # Set the emission strength
        
        # Add a Material Output node
        material_output_node = nodes.new(type='ShaderNodeOutputMaterial')
        
        # Connect the emission node to the material output
        material.node_tree.links.new(emission_node.outputs['Emission'], material_output_node.inputs['Surface'])
    else:
        material = existing_material
        # Update the existing material's color and strength
        nodes = material.node_tree.nodes
        for node in nodes:
            if isinstance(node, bpy.types.ShaderNodeEmission):
                node.inputs['Color'].default_value = (*color, 1.0)
                node.inputs['Strength'].default_value = strength
                break
    
    # Assign the material to the object
    if obj.data.materials:
        # If the object already has materials, replace the first one
        obj.data.materials[0] = material
    else:
        # If the object has no materials, append the new one
        obj.data.materials.append(material)

def lerp(a, b, k):
    return a + (b - a) * k

def color_lerp(color1, color2, k):
    r, g, b = lerp(color1[0], color2[0], k), lerp(color1[1], color2[1], k), lerp(color1[2], color2[2], k)
    return (r, g, b)

class Charge:
    def __init__(self, k: float, pos: Tuple[float, float, float]):
        """
        initialization method
        """
        self.k = k
        self.x = pos[0]
        self.y = pos[1]
        self.z = pos[2]
    def __call__(self, pos: Tuple[float, float, float]):
        posx = pos[0]
        posy = pos[1]
        posz = pos[2]
        r = sqrt((self.x - posx)**2 + (self.y - posy)**2 + (self.z - posz)**2)
        fieldx = -(self.k * (posx - self.x)) / (r**3)
        fieldy = -(self.k * (posx - self.y)) / (r**3)
        fieldz = -(self.k * (posx - self.z)) / (r**3)
        return (fieldx, fieldy, fieldz)

class ElectricField:
    def __init__(self, charges: List[Charge]):
        self.charges = charges
    def __call__(self, pos):
        x, y, z = 0, 0, 0
        for charge in self.charges:
            field = charge(pos)
            x += field[0]
            y += field[1]
            z += field[2]
        return (x, y, z)


for material in bpy.data.materials:
    if material.name[-1] == "E":
        bpy.data.materials.remove(material)
        
charges = []
for obj in bpy.context.scene.objects:
    if obj.name[-1] == 'E':
        charges.append(obj)
        
fields = []
for charge in charges:
    fields.append(Charge(charge['q'], charge.location))

sum = ElectricField(fields)

for obj in charges:
    k = obj['k']
    c1 = (0.7, 0.3, 0.1) # Change to your preference
    c2 = (0.1, 0.3, 0.7) # Change to your preference
    color = color_lerp(c1, c2, k)
    assign_emission_shader(obj.name, color, obj, s)